Matematyka Finansowa.pl

W ostatnim wpisie (Wartość przyszła pieniądza – oprocentowanie proste zmienne w czasie) przedstawiłem sposób rozwiązywania zadań, w których mamy do policzenia, np. odsetki od lokaty bankowej przy zmiennym oprocentowaniu, ale bez ich kapitalizacji w trakcie trwania lokaty. W rzeczywistości odsetki są bardzo często kapitalizowane w trakcie trwania lokaty. Zazwyczaj raz do roku w przypadku lokat kilkuletnich. Samo oprocentowanie jest zaś zmienne w czasie. Pokażę zatem jak podejść do rozwiązywania takich zadań.

Przykład 1:
Kowalski wpłacił rok temu 4 000 zł na lokatę bankową. Bank oferował półroczną kapitalizację odsetek oraz zmienne w czasie oprocentowanie. Początkowo wynosiło ono 10% w skali roku. Po 2 miesiącach zostało jednak obniżone do 9%, natomiast od 9 miesiąca trwania lokaty ponownie bank zaoferował 10%. Jakich odsetek Kowalski może się spodziewać (lokata kończy się dziś)?

Rozwiązanie takiego przykładu może wydawać się trudne, niemniej takie nie jest. Najłatwiej jest podzielić okres trwania lokaty na podokresy. Będzie ich tyle ile kapitalizacji oferuje bank w trakcie trwania lokaty. W naszym przypadku będą to dwa półroczne podokresy. Następnie dla każdego z nich wyliczamy średnie oprocentowanie. O tym jak to zrobić napisałem we wpisie na który się powołałem. Warto się z nim zapoznać. Tu umieszczę jedynie jeszcze raz wzór na obliczenie średniego oprocentowania:

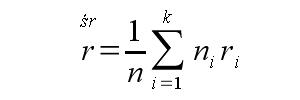
Obliczmy zatem średnie oprocentowanie dla każdego z podokresów:

I połowa roku:
r_śr = 1/(1/2) * [(2/12 * 0,10) + (4/12 * 0,09)]
r_śr = 2 * 0,0467
r_śr = 9,34%
Średnie oprocentowanie w pierwszej połowie roku wynosiło 9,34% (w skali roku)

II połowa roku:
r_śr = 1/(1/2) * [(3/12 * 0,09) + (3/12 * 0,10)]
r_śr = 2 * 0,0475
r_śr = 9,50%
W drugiej połowie roku średnie oprocentowanie wyniosło 9,50% (w skali roku).

Skoro mamy już oprocentowanie lokaty w obu podokresach, możemy obliczyć ile zarobi Kowalski. Poniższy wzór służy do obliczania przyszłej wartości pieniądza dla oprocentowania zmiennego w czasie oraz przy założeniu wielokrotnej kapitalizacji.

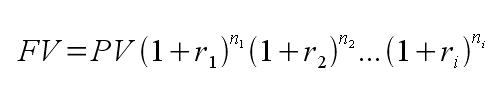
Oznaczenia:
FV – wartość przyszła (Future Value)
PV – wartość bieżąca (Present Value)
n₁, n₂, …, n_i – ilość okresów kapitalizacji z danym oprocentowaniem r_i
r₁, r₂, …, r_i – średnie oprocentowanie dla kolejnych okresów kapitalizacji

Podstawiamy teraz dane z zadania do powyższego wzoru:
FV = 4 000 zł * (1 + 0,0934/2)¹*(1 + 0,095/2)¹
FV = 4 385,53 zł
Kowalski otrzyma z banku 4 385,53 zł. Jego zysk wyniósł zatem niecałe 400 zł.

Przykład 2:
Na początku 2007 roku Kowalski założył w banku konto oszczędnościowe. Odsetki były kapitalizowane kwartalnie. Poniżej zamieszczono oprocentowanie konta w kolejnych miesiącach. Jakiej kwoty klient banku może spodziewać się na koncie na początku 2008 roku jeśli dwa lata wcześniej wpłacił 10 000 zł?
Oprocentowanie konta oszczędnościowego:
styczeń – lipiec 2007: 5,00%
sierpień – listopad 2007: 5,50%
grudzień – marzec 2008: 6,50%
kwiecień – październik 2008: 7,00%
od listopada 2008: 8,00%

Policzmy średnie oprocentowanie konta oszczędnościowego w kolejnych kwartałach (począwszy od pierwszego kwartału 2007 roku).
r1 = 5,00%
r2 = 5,00%
r3 = 1/(1/4) * [(1/12 * 0,05) + (2/12 * 0,055)] = 5,33%
r4 = 1/(1/4) * [(2/12 * 0,055) + (1/12 * 0,065)] = 5,83%
r5 = 6,50%
r6 = 7,00%
r7 = 7,00%
r8 = 1/(1/4) * [(1/12 * 0,07) + (2/12 * 0,08)] = 7,67%

Pamiętać należy, że powyżej obliczone oprocentowanie jest oprocentowaniem w skali roku.
Podstawiamy teraz obliczone dane do wzoru zamieszczonego w tym wpisie:
FV = 10 000 zł * (1 + 0,05/4)²*(1 + 0,0533/4)¹*(1 + 0,0583/4)¹*(1 + 0,065/4)¹*(1 + 0,07/4)²*(1 + 0,0767/4)¹
FV = 11 130,17 zł
Kowalski zatem zarobił w banku ok. 130 zł przez 2 lata.