W jednym z poprzednich wpisów (Wartość przyszła pieniądza – oprocentowanie proste zmienne w czasie) przedstawiłem sposób rozwiązywania zadań, w których spotykamy się ze zmienną w czasie stopą procentową. Wprawdzie zamieściłem tam wzór na policzenie średniej stopy procentowej, niemniej warto tematykę tę rozszerzyć.
Zacznijmy może od definicji. Przeciętna (średnia) stopa procentowa jest to taka stopa procentowa, zazwyczaj roczna, przy której początkowy kapitał osiągnie wartość identyczną z tą, jaką osiągnąłby ten sam kapitał przy zmiennych w czasie stopach procentowych.
Przypomnijmy sobie także wzór niezbędny do wyliczenia przeciętnej stopy procentowej:
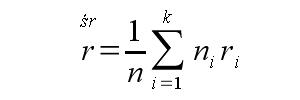
Przykład 1:
Kowalski wpłacił 10 000 zł na roczną lokatę bankową. Bank zaoferował oprocentowanie progresywne – początkowo wynosi 4%, ale po każdym kwartale zwiększane jest o 0,5 pkt. proc. Jakich odsetek Kowalski może się spodziewać po roku (bank stosuje kapitalizację na koniec okresu deponowania)?
Rozwiązanie takiego przykładu jest bardzo proste. Skorzystamy z powyższego wzoru:
rśr = 1/(1) * [(3/12 * 0,04) + (3/12 * 0,045) + (3/12 * 0,05) + (3/12 * 0,055)]
rśr = 1 * 0,0475
rśr = 4,75%
Średnie oprocentowanie lokaty wyniosło 4,75% (w skali roku).
Policzmy jeszcze w jakiej kwocie odsetki otrzyma Kowalski:
FV = 10 000 zł * (1 + 0,0475)1
FV = 10 475 zł
Kowalski otrzyma z banku 10 475 zł. Jego zysk wyniesie zatem 475 zł.
Przykład 2:
Dokładnie rok temu Kowalski założył dwuletnią lokatę w banku A na kwotę 2 000 zł z oprocentowaniem stałym w wysokości 5% i kapitalizacją na koniec okresu deponowania. Aktualnie konkurencyjny bank B oferuje lokaty roczne z oprocentowaniem w wysokości 6,50%. Kowalski zastanawia się nad zerwaniem lokaty w dotychczasowym banku i przeniesieniem ich do nowego. Czy będzie to operacja opłacalna? Bank A za zerwanie lokaty pobiera opłatę w wysokości 20 zł, ale za to zwraca odsetki naliczone do dnia zerwania lokaty.
Rozwiązanie takiego przykładu może wydawać się skomplikowane, ale w rzeczywistości takie nie jest. Gdyby Kowalski nie skorzystał z oferty banku B, otrzymałby 200 zł odsetek z banku A w przyszłym roku. Co jednak, gdyby chciał skorzystać z oferty banku B? Policzmy najpierw jaką kwotę będzie mógł wpłacić na lokatę:
PV = 2 000 zł * (1 + 0,05)1
PV = 2 000 zł * 1,05
PV = 2 100 zł
Odejmijmy jeszcze 20 zł opłaty za zerwanie lokaty. Tym samym Kowalski przez rok zarobił rzeczywiście 80 zł (4%).
Teraz policzmy ile zarobi Kowalski wpłacając oszczędności do banku B:
FV = 2 080 * (1 + 0,065)1
FV = 2 080 * 1,065
FV = 2 215,20 zł
Zmiana banku jest dla Kowalskiego korzystna. Trzymając środki w banku A zarobiłby 200 zł, przenosząc je do banku B zarobi łącznie 215,20 zł.
Policzmy jeszcze średnie roczne oprocentowanie przy uwzględnieniu zmiany banku i kapitalizacji dwuletniej. Z uwagi na karę w wysokości 20 zł nie możemy użyć wzoru z początku wpisu. Poradzimy sobie jednak inaczej:
rśr = (1/2) * 215,20 / 2 000
rśr = (1/2) * 0,1076
rśr = 0,0538
rśr = 5,38%
Kowalski zmieniając bank uzyska średnie oprocentowanie w wysokości 5,38%. Jest to więcej niż początkowe 5% oferowane przez bank A.
1 Komentarze.