Matematyka Finansowa.pl

Jakiś czas temu opisałem efektywną stopę zwrotu. Tematykę warto kontynuować. Efektywna stopa zwrotu nie jest bowiem jedyną występującą w matematyce. Równie popularna jest księgowa stopa zwrotu, która używana jest w szczególności przy ocenie atrakcyjności projektów inwestycyjnych.

Księgowa stopa zwrotu (ARR – Accounting Rate of Return) jest wartością procentową. Wyraża ją stosunek zysku netto osiągniętego dzięki zrealizowanej inwestycji do nakładów poniesionych na jej realizację. Oceniając opłacalność projektów inwestycyjnych wybieramy ten, dla którego wskaźnik ARR jest wyższy. Trzeba mieć jednak na uwadze, że ARR jest bardzo prostym wskaźnikiem, nie powinien być zatem jedynym używanym do określania atrakcyjności inwestycji. O ile bowiem łatwo przewidzieć koszty związane z inwestycją, to już zyski są tylko hipotetyczne.

Przykład 1:
Kowalski otrzymał propozycję inwestycji w firmę X. Kwota inwestycji to 10 000 zł, spodziewany zysk zaś wynosi 1 500 zł rocznie. Oblicz ARR.

Zapoznajmy się jeszcze z wzorem na wyliczenie księgowej stopy zwrotu:

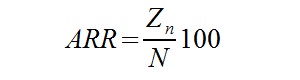
Oznaczenia:
Z_n – roczny zysk netto, osiągnięty dzięki poniesionym nakładom inwestycyjnym
N – wartość nakładów inwestycyjnych

Aby rozwiązać zadanie podstawiamy dane do wzoru.

ARR = (1 500 / 10 000) * 100
ARR = 0,15 * 100
ARR = 15%

Przykład 2:
Firma ma do wyboru dwie inwestycje. Pierwsza, to zakup prostej maszyny produkcyjnej. Jej cena to 50 000 zł. Maszynę można szybko kupić i przygotować do pracy, spodziewane zyski wynoszą 20 000 zł rocznie przez najbliższe 3 lata, później maszyna ulegnie zużyciu. Drugą opcją jest zakup zdecydowanie droższej maszyny, ale o 5-letnim okresie trwałości. Kosztuje ona 70 000 zł i przełoży się na roczny wzrost zysku przedsiębiorstwa o 25 000 zł. Zakup której maszyny jest bardziej opłacalny?

Policzmy księgową stopę zwrotu dla obu inwestycji.

ARR₁ = (20 000 / 50 000) * 100
ARR₁ = 0,40 * 100
ARR₁ = 40%

ARR₂ = (25 000 / 70 000) * 100
ARR₂ = 0,3571 * 100
ARR₂ = 35,71%

ARR dla pierwszego wariantu jest korzystniejsze, niemniej to druga inwestycja będzie bardziej opłacalna. Dlaczego? Otóż pierwsza maszyna będzie funkcjonować jedynie 3 lata, przedsiębiorstwo, po uwzględnieniu poniesionych nakładów, zarobi na niej 10 000 zł. Druga zaś będzie funkcjonować przez 5 lat, przyniesie w tym okresie zysk na poziomie 55 000 zł. Zadanie to idealnie pokazuje, że księgowa stopa zwrotu nie powinna być jedynym wyznacznikiem opłacalności inwestycji.

Przykład 3:
Przedsiębiorstwo planuje przeznaczyć 45 000 zł na projekt inwestycyjny. Warunkiem jest, aby wskaźnik ARR był wyższy od 20%. Jaki dodatkowy zysk roczny musi wygenerować inwestycja, alby mogła być zrealizowana przez przedsiębiorstwo?

W tym zadaniu mamy daną ARR, poszukujemy zaś Z_n. Przekształćmy zatem powyższy wzór i podstawmy wymagane dane.

ARR = Z_n / N * 100
Z_n = ARR * N / 100
Z_n = 20 * 45 000 / 100
Z_n = 9 000

Spodziewany dodatkowy zysk netto musi być wyższy od 9 000 zł, aby inwestycja mogła być zrealizowana przez przedsiębiorstwo.